分布式深度学习-Survey

Intro

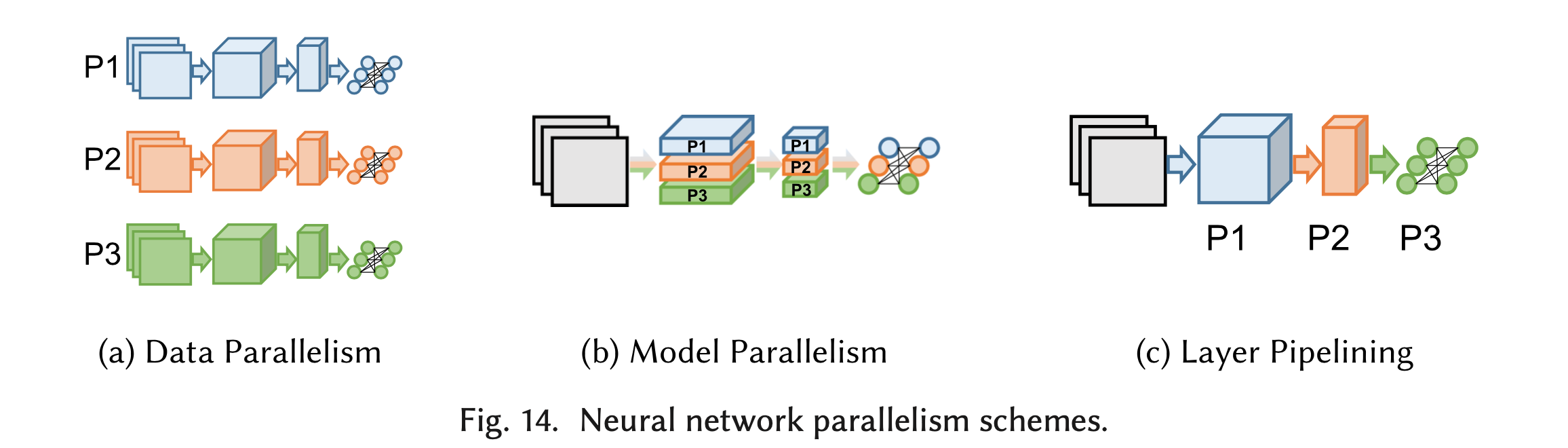
由于神经网络的规模越来越大，单个计算设备往往难以在短时间内完成对整个网络的训练，因此出现了大量的分布式神经网络训练方案，利用多个节点的计算能力加速训练过程。 而计算设备也在不断更新，可以是CPU、GPU以及TPU等更多类型的硬件。本文调研了分布式深度学习领域相关的最新文献，简要介绍该领域目前关注的主要问题和已有的解决方案。 文章的内容安排如下：第2节简要介绍背景知识，包括机器学习和深度神经网络的基本概念、SGD算法的细节；第3节介绍深度神经网络的性能模型；第4到7节分别介绍图14所示三种分布式训练的并行方案：数据并行、模型并行和流水线并行，以及结合多种方案的混合并行。第8节介绍寻找最优并行策略一般采用的算法；第9节介绍对数据传输过程进行优化的主要方法。本文图片及2、3、4、9节部分内容，参考自[81]。

Background

机器学习和深度神经网络

这一节将简要介绍机器学习的相关概念，以及深度神经网络和机器学习的关系。

机器学习可以分为监督学习、无监督学习、半监督学习等。监督学习是指从标注数据中学习预测模型的问题。 标注数据表示输入输出的对应关系，预测模型对给定的输入产生相应的输出。监督学习的本质是学习输入到输出的映射的统计规律。无监督学习则是从无标注数据中学习一定模式的问题。半监督学习则是采用一部分标注数据和一部分无标注数据进行学习的问题。我们经常看到的图片分类、语音识别等，大多都是监督学习问题。

监督学习问题的一般框架如下：

• 输入：n个独立同分布（i.i.d.）的训练数据$(x_i,y_i)\in \mathcal{X} \times \mathcal{Y}, i=1,…,n$。 在回归问题中，$Y$是连续的；在分类问题中，$Y$是离散的。例如对于图片分类问题，$ \mathcal{X}$ 可以是32x32的图片的集合，$ \mathcal{Y}$ 可以是标注图片类别的标签。

• 目标函数：$f \in F$。一个机器学习模型，可以表示为一个目标函数$f$，带有一些参数，用$\theta$表示，$\theta \in \mathbb{R}^d$。
• 损失函数：$L(f;x,y)$ 。常用的损失函数有0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等。我们希望损失函数是可导的，以便于对参数进行优化。

• 期望风险（expected risk）：$R_{exp}(f)=\int L(f;x,y)dP(x,y)$。这是理论上模型$f(X)$关于联合分布$P(X,Y)$的平均意义下的损失。与此相对的，存在一个经验风险（empirical risk）：$R_{emp}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i))$。经验风险是在训练数据集上得到的平均损失。根据大数定理，当样本容量N趋于无穷时，经验风险$R_{emp}(f)$趋于期望风险$R_{exp}(f)$。

• 学习任务（task）：数据域$\mathcal{X} \times \mathcal{Y}$上的数据分布$\mathcal{D}$，带有参数$\theta$的目标函数$f$，损失函数$L(f;x,y)$共同构成了一个学习任务。我们的目标就是找到某个参数$\theta$，使得期望风险$R_{exp}(f)$尽可能小。由于我们往往只能得到n个训练数据，根据大数定理，我们一般求解经验风险，作为期望风险的预测值。

神经网络是模拟生物大脑结构和功能而产生的一种计算模型，可以看做是以上框架中目标函数的一种。神经网络由大量神经元连接构成，每个神经元就是一个简单的函数，对输入数据进行处理后传输给下一个神经元。近年来，神经网络的深度不断增加，使其可以表达更加复杂的层次化信息，在越来越多的领域得到广泛应用。

随机梯度下降算法 SGD

对神经网络进行训练的最常用算法是随机梯度下降算法（SGD）[1]。

第一行规定了运行SGD的次数，即终止条件或computational budget。一般来说，实际的机器学习应用的终止条件可能是固定的迭代次数、固定的运行时间，或达到某个准确率。第二行是从数据集$S$中随机采样一个样本。第三行是计算损失函数$l$在参数$w^{(t)}$下的梯度。上标$t$代表第$t$次迭代。每一层（例如第$i$层）的梯度$w_{i}^{(t)}$是通过反向传播得到的。第四行是用某种权重更新规则$u$，根据得到的梯度值以及之前的权重值来更新权重。

权重更新规则

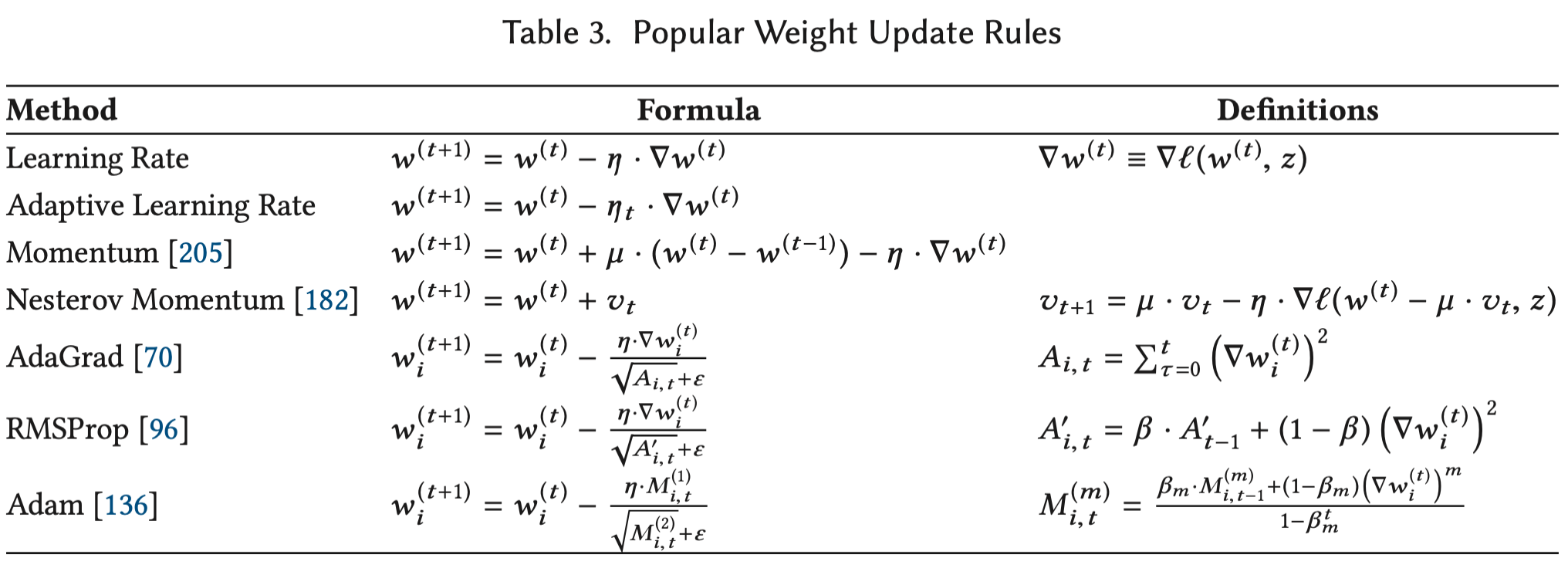
权重更新规则可以被定义为梯度$g$、之前的权重$w^{(0)},…,w^{(t)}$以及当前迭代次数$t$的函数。主要有以下几种：

• Learning Rate。最基本的SGD update rule。$\eta$ 代表学习率，控制着梯度值对下一轮权重参数的影响程度。
• Adaptive Learning Rate。通常学习率被设置为固定值，但有时候也会设置一个跟迭代次数相关的学习率$\eta_t$ ，随着迭代次数逐渐降低。
• Momentum，动量法。使用当前权重和过去权重的差值$w^{(t)} - w^{(t-1)}$ 来避免局部最小和多余步骤。
• RMSProp、Adam等。使用梯度的一阶矩、二阶矩来适应每个权重参数的学习率，增强了稀疏更新的能力。
• 表格中的所有系数都被称作超参数。为了得到最好的结果，超参数是需要根据具体应用进行调整的。

Minibatch SGD

实际使用SGD时，更常用的是Minibatch SGD，从数据集的一个子集（而不是一个样本）中得到梯度的平均值。Minibatch SGD代表了SGD（一次计算一个样本）和batch GD（一次计算整个数据集）之间的tradeoff。

Minibatch SGD的实现方法是，随机打乱数据集，每次处理连续的B个样本，完整遍历数据集一次被称作一个epoch。

Generalization vs Utilization

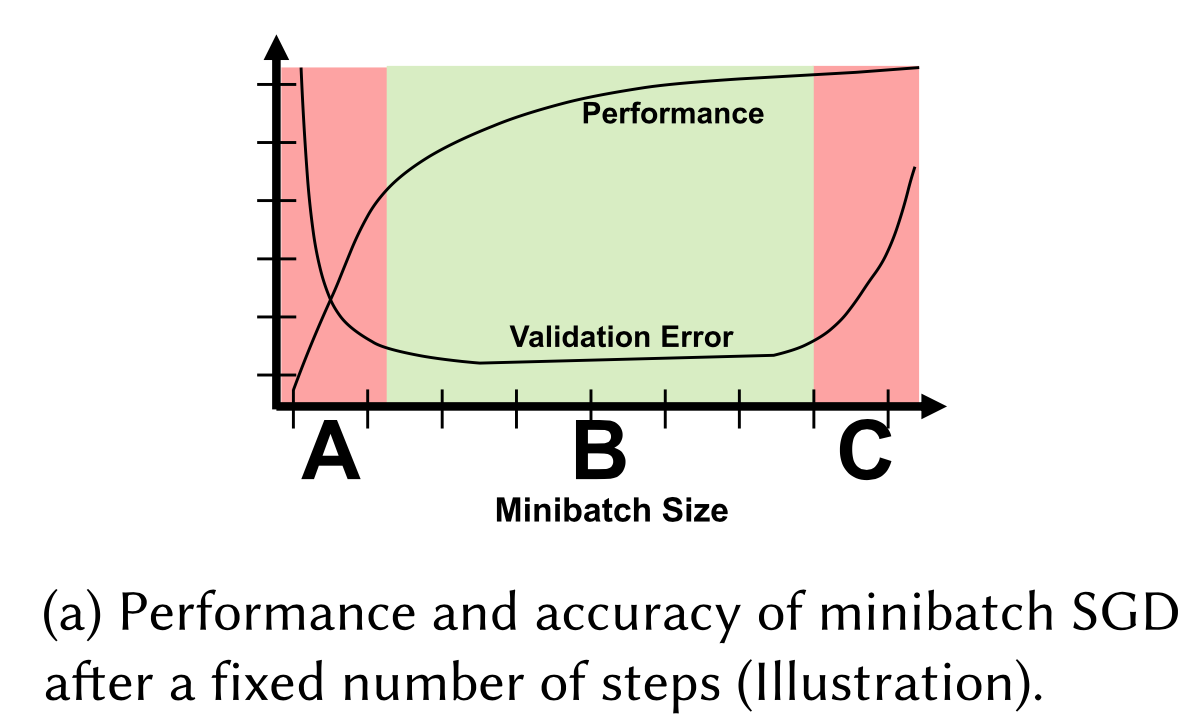
Generalization指的是模型的准确率，Utilization指的是硬件的利用率。如何设置minibatch size是一个复杂的问题，因为它不仅会影响模型的准确率，也会影响硬件的利用率。

如图所示，minibatch size不能太小（区域A），太小的minibatch size不仅会导致很低的硬件利用率，也会产生较大的Validation error。也不能太大（区域C），当minibatch size增加至超过某个界限后，硬件利用率并无明显增加，而Validation error却会增加。

性能模型 Performance Model

要研究分布式深度学习，很多时候我们都需要一个深度神经网络的性能模型。有了性能模型，就能指导我们进行网络的设计、分布式部署方案的设计、寻找最优的模型划分策略等等。但设计一个神经网络的性能模型并不容易。

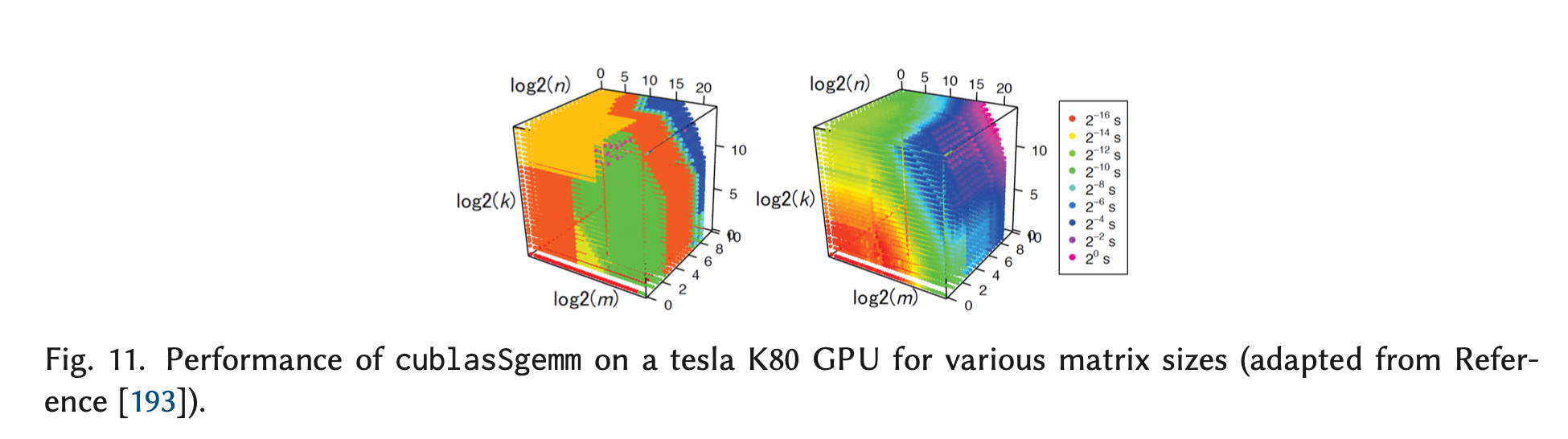
最大的难点在于，对组成神经网络的op进行时间建模。因为op的性能模型往往是非线性的。大多数op都会调用低层加速库中实现好的kernel，图11是CUBLAS库中矩阵乘的数据[2]，可以看出，运算时间并不随数据大小线性改变，因为CUBLAS会从15种矩阵乘的实现中，根据具体的矩阵大小，选择性能最好的一种。

对深度神经网络的时间进行建模，主要关注以下几类运算时间占比最高的op：对于卷积网络，是全连接层和卷积层，对于循环网络，是循环单元。其中，卷积层的建模尤其复杂。

全连接层

全连接层可以被看做是矩阵-矩阵乘。因此，高效的线性代数库都可被使用，例如CUBLAS、MKL、ESSL。BLAS GEMM还可在批处理时被使用。

卷积层

卷积可以被直接计算，但这会使得在向量处理器或多核架构下的硬件利用率极低，这些硬件大多都有对并行的乘法累加运算进行优化。文章[3]指出，如果不对卷积算法本身进行改进，可以通过对运算进行重排序或引入冗余数据来最大化数据的重用率，从而提高硬件利用率，这篇文章还分析了卷积和池化op的数据传输量的下界，并进一步分析了怎样才能通过循环的重新组织和tiling达到下界。

但比较常见的卷积层优化，是从卷积算法本身来进行的。最常见的三种对卷积算法的改进：

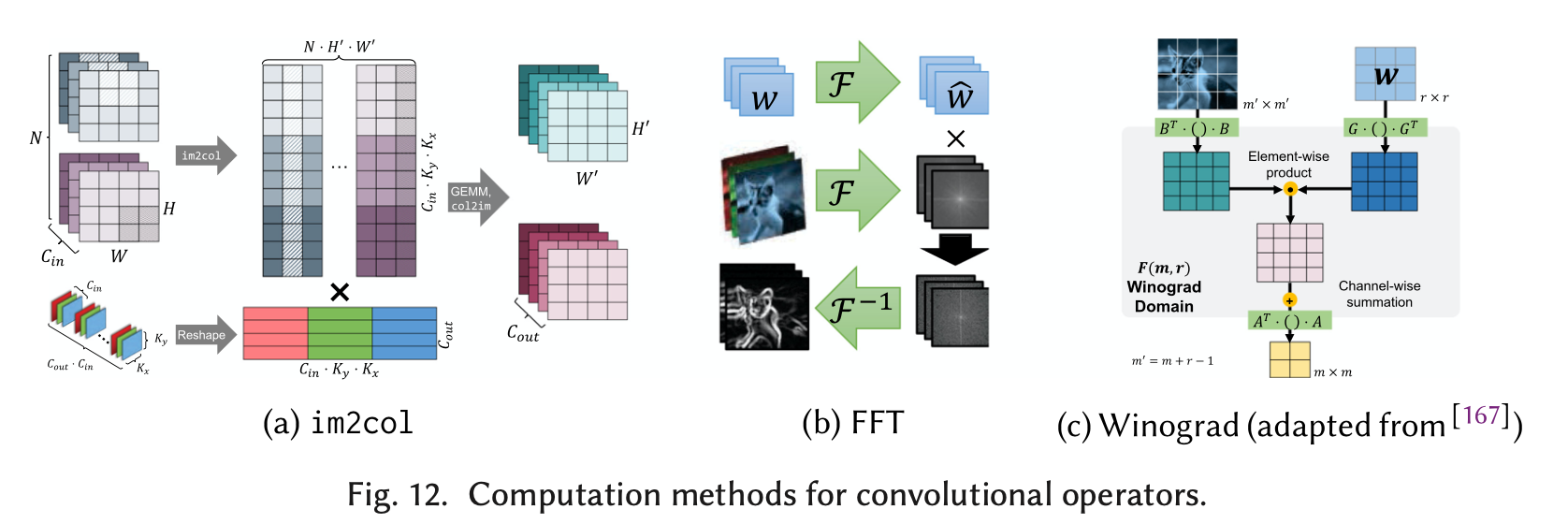
图12(a)是方案1，把卷积操作转化为矩阵乘法（通过使用Toeplitz 矩阵, 这一过程也叫做im2col），然后采用GEMM。其具体操作是，把输入的图像从3D tensor转化为2D矩阵，矩阵中的每一行都是被展开的要被卷积的一个patch，（这样的转化会产生一些数据冗余，因为被多次卷积的数据会被多次展开）；把多个卷积核存储为一个2D矩阵，矩阵的每一列都是一个被展开的卷积核，把两个矩阵相乘后的结果再转化成3D tensor，就是卷积后的结果。还有另一种与im2col对应的方案叫做kn2row[3]。由于上述方案会消耗大量的内存（因为要保存转化后的矩阵），cuDNN在实际实现中提供了implict_GEMM和precomp_GEMM。在implicit_GEMM中，Toeplitz矩阵并不会真的实例化。也有文章[4]使用Strassen矩阵乘法来进行优化。

图12(b)是方案2，FFT。文章[5]指出，卷积核越大，FFT的收益就越大。除此之外，也能通过一些DNN特有的性质来对FFT算法进行改进，从而在DNN上实现更大的加速。文章引入两种FFT卷积的实现，分别基于cuFFT（闭源）和fbfft（自主实现，开源）。最后实现的性能比NVIDIA的cuDNN中的实现更好。 （因为这篇文章发表的时间较早（2015），尚不确定最新的cuDNN是否已对fft进行改进。）

图12(c)是方案3，Winograd算法[6]。因为FFT适用于大的卷积核，因此这篇文章使用Winograd算法提出了一种适用于小卷积核的卷积算法。而且，由于在Winograd算法中，运算次数随着卷积核大小的增长而平方增长，该方法也只适用于小的卷积核。

文章[5] [6] [7]的实验结果表明，并没有“one-size-fits-all” 的卷积算法。

数据的布局（layout）对性能的影响也很大。文章[8] 指出把数据从$N×C×H×W$ tensors 转化为$C ×H ×W ×N $ tensors，卷积和池化操作会被计算地更快。

DNN加速库，例如cuDNN、MKL-DNN提供了多种卷积算法和数据布局方案，并且提供了一些函数来帮助用户在给定tensor大小和内存限制的条件下选择最佳算法。在实现时，这些函数可能将每一种算法跑一遍，进而选择性能最好的。

循环单元（recurrent units）

在RNN units内部往往有各种复杂的门结构，包含一些矩阵运算或element-wise操作。RNN的并行可以分为两大类：层内的并行、层间的并行。

层内的并行：文章[9]给出了几种针对RNN的优化。（1）把RNN units内部所有的计算融合成一个function(kernel) ，把中间结果保存在scratch-pad memory中，不仅减少了kernel调度的开销，也节省了到global memory中取数据的次数。（2）矩阵的预转换（pre-transposition）（3）在GPU的不同处理器上并发执行独立的循环单元。

层间的并行可以通过pipeline来实现。

其他的对于RNN的优化还有：从内存开销的角度进行优化，文章[10]提出用动态规划来平衡缓存中间结果和重新计算。文章[11] 在卷积op上实现了类似的效果。文章[12]提出了Persistent RNN，解决了提高GPU利用率的两个限制：小的 minibatch sizes和长序列输入。这个方案也减少了RNN的内存占用，使得用户可以搭建更深的RNN网络。

网络总时间建模的相关文章

文章[13]提出的Performance model为：神经网络总的计算时间=各层时间之和，每层时间=前向计算时间+后向计算时间+权重更新时间。假设每个layer均匀分布在多个设备之间，取时间最长的segment的时间为该layer的时间。每一个时间又分为计算时间+数据传输时间。在对前向计算时间和后向计算（梯度计算）进行建模时，关注layer之中的神经元数量，通过神经元数量估算乘法次数，再根据单次乘法时间计算总时间。

文中分别对模型并行和数据并行进行了建模。

• 模型并行 对神经网络layer $l$ 的segment $p$ 的前向计算时间建模为：

  

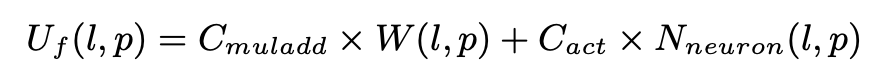
  $C_{muladd}$ 是一次乘加操作的时间。$W(l,p)$是从layer $l-1$ 连接到layer $l$ 中的神经元的所有weight的数量。$C_{act}$ 是在神经元上执行的非线性函数$f(x)$的时间。$N_{neuron}(l,p)$ 是layer $l$ 的 segment $p$ 中的神经元数量。

  对数据传输的时间建模为：

  

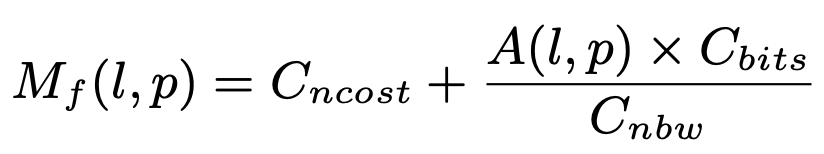
  $C_{ncost}$ 是网络的延迟。$C_{nbw}$ 是带宽。$A(l,p)$ 是segment $p$ 从layer $l-1$ 接收到的activation的数量，$C_{bit}$是activation的大小，两项相乘就是接收到的总数据量。对于传输时间的建模比较trivial。对于前向计算时间的建模过于理论化，忽略了在实际实现时的不同算法的区别。

  对反向传播的时间建模为：

  

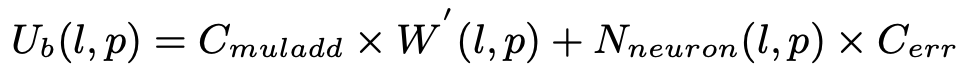
  $W^{‘}(l,p)$是从layer $l+1$ 连到layer $l$ 的连接数量。$C_{err}$ 是error function 的计算时间。（个人理解为求导时间。）

  对参数更新时间的建模：

  

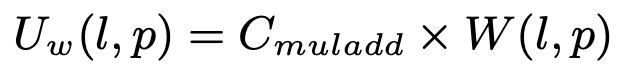
• 数据并行 数据并行又分为三种模式。

  • Chip-level Multiprocessing。定义interference factor $C_{interf} (H(l))$ 来表示多线程之间的干扰（例如访存带宽竞争）。通过运行一个小型的benchmark来估算干扰因子。最终的时间估计值就是用干扰因子乘以单线程的时间。

  • Layer Replication

  • Multiple Model Replicas - Parameter Server。主要的变化在于引入了Parameter Server。写更新到PS可以异步执行，但是读出最新的参数是同步的。通过建模最坏情况下的时间（所有worker同时使用带宽）和最好情况下的时间（只有一个worker使用带宽），实际的实现中，真实时间介于二者之间，因为不同的实现方式的具体的硬件条件会导致数据传输和计算过程不同程度的overlap，使得总时间难以准确估计。

文章[2]是对异步的SGD进行时间建模。这篇文章指出，上述文章[13]不能应用于非PS架构的分布式环境（例如采用all-reduce在节点之间进行数据同步），也不能应用于异步的SGD。文章[2]提出的Performance model不仅能预测一个epoch的训练时间，也能预测异步SGD训练过程中的mini-batch size和staleness。

这篇文章对时间的建模的方法是：先构建经验模型，然后通过实际测得的时间和最小二乘法对经验模型中的未知系数进行拟合。不同于其他工作中通过硬件参数和浮点运算次数等信息来对运行时间做预测，这篇文章使用了经验模型+拟合的方法。但是这篇文章的Performance Model不准确，因为他们假设了卷积核的大小为3x3，忽略了其他大小的卷积核。

对前向计算和后向更新的时间建模，是通过对执行其计算过程的底层CUDA kernel和SGEMM kernel的时间进行建模。对CUDA库中的im2col的建模如下：

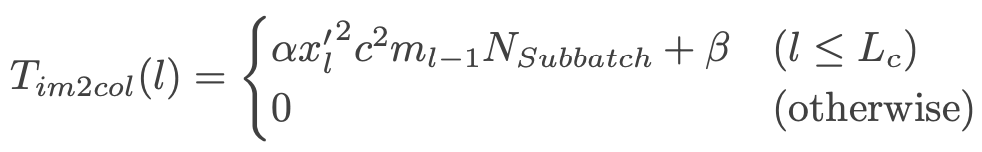
cublasSgemm的建模并不trivial，因为作者发现cublasSgemm矩阵乘法的Performance并不是随着输入矩阵大小连续变化的。这可能是因为sub-kernels根据特殊的参数进行了特殊的优化。于是这篇文章先测得大量的cublasSgemm的矩阵乘数据，包含的矩阵大小为$(a^x, a^y, a^z)$ (表示$a^x\times a^z$ 和$a^z \times a^y$ 两个矩阵相乘)，其中$a$是一个常数，$x,y,z = 0,1,2…$。接下来构建许多个线性模型，对于 $m\times k$ 和 $k\times n$ 的矩阵乘法，线性模型包含的项为：${mnk, mn, mk, nk, m, n, k}$， 以及浮点运算次数($O(mnk)$) 和最小访存次数 ($O(mn + mk + nk)$)。在拟合线性模型中的未知参数时，使用$\log m,n,k$ 空间中的8个邻居点。因此每个线性模型都有一个有效范围，在针对具体某个矩阵乘进行预测时，使用有效范围包含该测试点的线性模型。之所以要构造很多个线性模型是因为单个线性模型不能拟合出cublasSgemm的non-trivial规律。

Paleo[14]构建了更为详细的Performance model。其总体示意图如下：

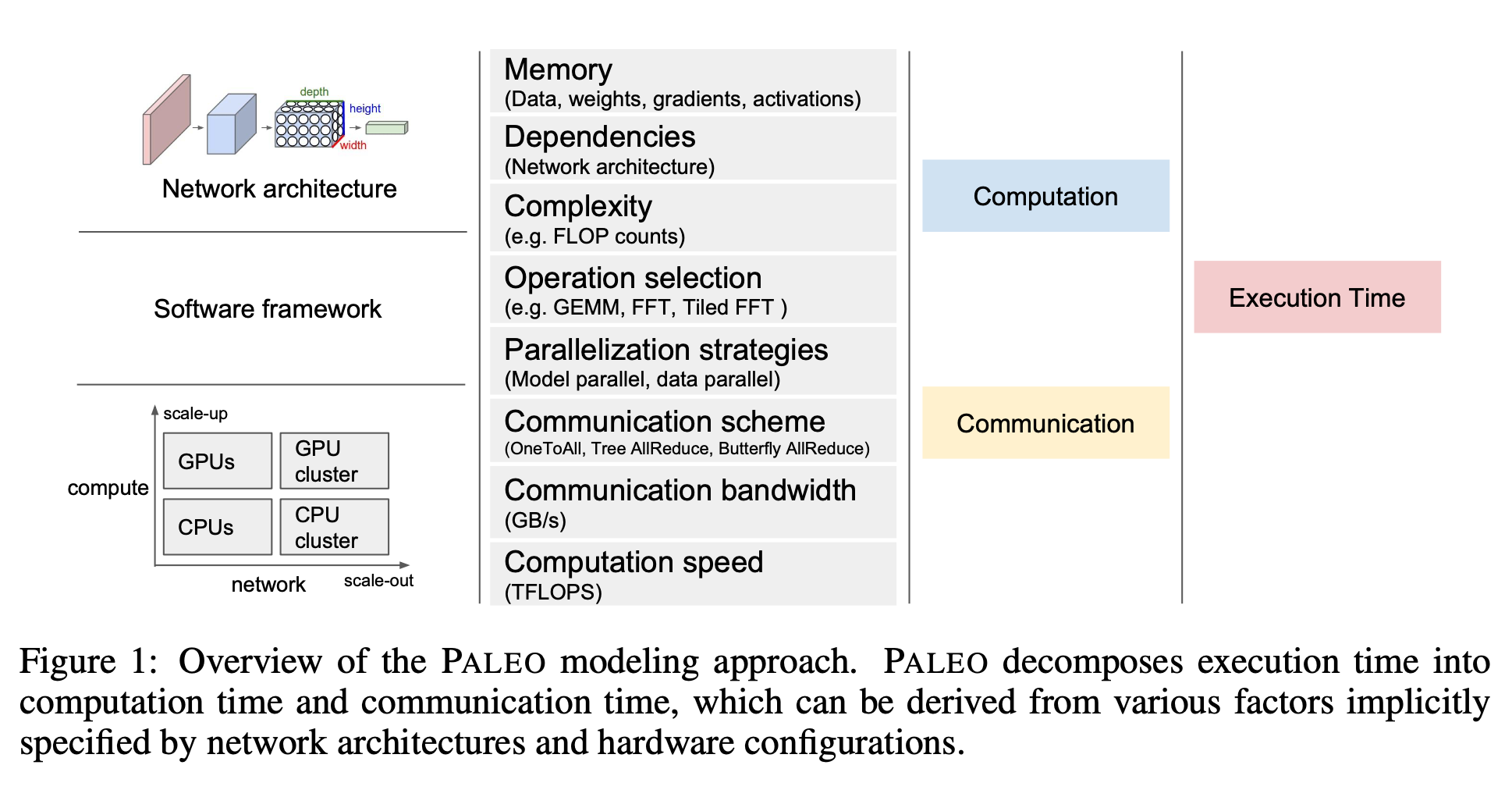
总时间由计算时间和数据传输时间组成。影响计算时间的因素又包括：输入数据的大小（由网络结构决定）、网络各个layer实现时所采用的算法的复杂度、硬件参数等。数据传输时间则跟网络层与层之间的依赖关系、硬件带宽和并行策略等有关。

我们最关心的是对卷积层的建模。其对卷积核的建模分为矩阵乘和FFT两种，这篇文章分别从理论层面估算两种方法各所需的浮点运算次数，再根据硬件的实际浮点运算速度，相除得到预测时间。Paleo通过一个offline benchmark进行测试，定义一个Heuristic来在两种算法之间进行选择。

他们的框架需要输入网络的参数以及硬件的各项参数。由于实际的硬件性能并不总是能达到峰值，他们还提出了一个指标：Platform Percent of Peak（PPP），通过一个小型的benchmark找到当前硬件性能占峰值的比例系数，再用Performance model乘以这个系数，即可得到实际的性能预测值。

NeuralPower[15]团队的工作是基于Paleo来做的，他们对神经网络时间的建模侧重于推理阶段而不是训练阶段。但他们没有提出一个基于分析的理论模型，而是使用了基于学习的多项式回归方法。对神经网络op的各项参数，例如输入数据大小、输出大小、卷积核大小、步长等，结合另一些硬件参数，例如访存次数、浮点运算次数等，直接构建一个多项式模型，再使用Lasso回归进行模型拟合。NeuralPower比Paleo更加通用。但模型拟合的时间开销较大。

文章[16]直接用一个神经网络来预测其他神经网络的运算时间。文章[17]通过浮点操作次数来构建了Performance model，并使用performance model选择满足精度要求的性能最好的网络来满足用户的实时性要求。

以上文章基本都是着眼于对单个layer的时间进行建模，以及对分布式环境下的数据传输时间进行建模，对于网络总时间的建模方法往往比较简单，一般是把网络总时间看成各个layer的时间之和。但是对于更加复杂的分布式环境，这样的建模方法不一定准确。FlexFlow[53]对于这个问题有一个比较好的解决方案。

FlexFlow为了对某种划分方式下的网络运行总时间做预测，设计了一个task graph。他们把神经网络中每个op抽象为一个task（如果op被划分成几个部分，就抽象为几个task），把节点之间的数据传输也抽象为task。task就是task graph中的node，而task graph中的edge，代表了op之间的依赖关系。

每个task包含几项数据：exeTime readyTime startTime endTime等，exeTime是该task的执行时间。对于数据传输task，exeTime是数据传输时间。FlexFlow在构造任务图时，使用一个类似Dijkstra的最短路径算法，来给每个task的其他数据进行赋值。Task准备好时（所有前序任务已经结束），就会被enqueue到一个priority queue，并且会按照readyTime的顺序进行dequeue。类似于Dijkstra算法中，每次将被搜索到的节点的邻居节点加入边缘集合的操作。通过这样的方式，最后一个task被dequeue时，就能得到整个任务图的运行时间。

• 对Performance Model的benchmark的设计
  • 文章[16]：测试TensorFlow中的tensorflow.layers.conv2d op，使用不同的参数组合。参数的范围是：batch_size = [1, 64], in_wid = [1, 512], kernel_size = [1, 7], 以及多种stride和padding，以及是否存在bias。总共10,038,745,006,080种组合，从中任意选择50000组数据作为训练数据，80%作为训练集，10%作为测试集，10%作为验证集。
  • 文章[15]：AlexNet, VGG-16, VGG-19, R-CNN, NIN, CaffeNet, GoogleNet, overfeat and so on. 总计858 个卷积op, 216池化op, and 116全连接op
  • 文章[14]：AlexNet, VGG.
  • 文章[2]：自己构造的网络CNN-A, CNN-B, CNN-C .
  • 文章（Performance Evaluation）：AlexNet, VGG-19, GoogleNet, Resnet50, SqueezeNet.

数据并行

数据并行是最简单直观的并行方案，实现起来难度最小。其核心思想是，在多个计算设备上部署相同的完整神经网络，每个设备利用训练数据的一部分进行训练并计算梯度，在每个batch的数据计算完成后，通过一定的策略在多个设备之间完成参数的同步和更新。这样一来，每个设备的计算量并不大，同时多个设备之间不存在数据依赖，是并行计算的，使得总的时间开销呈近似线性减小。

神经网络中的几乎所有op（除了batch normalization）一次只对一个样本做运算，不存在对多个样本的处理（即使是对一整个batch的数据做处理，数据之间也可以看做是并行处理），因此可以把一个minibatch中的样本分为几部分，指定给多个设备来处理。神经网络的这一特点很适合用数据并行来加速前向计算和后向计算过程。

但在权重更新阶段，需要把多个设备的结果平均起来得到整个minibatch的梯度，这会引入多个设备之间的数据传输，通信开销可能成为瓶颈。例如，文章[18]提到，在VGG-16网络上，数据并行的传输开销占到了总时间的85%。因此，近几年各大会议上关于分布式机器学习的文章，主要是集中在优化数据并行的传输和同步开销，通过设计更加合理的调度方案、压缩传输的数据量等方式优化数据传输时间。

同时，数据并行还要求在每个计算节点都保存网络的参数，这意味着网络参数会被复制为很多份，存储开销也比较大。除此之外，文章[19]指出，数据并行不能处理样本较大的数据集。因为数据并行不存在对网络本身的划分，每个样本都要完整地存储进GPU或其他计算设备的内存中，这使得对于样本较大的数据集，如果采用数据并行，就不能使用很大的batch size。

中心化/去中心化

数据并行的架构，主要分为两大类：中心化和去中心化。

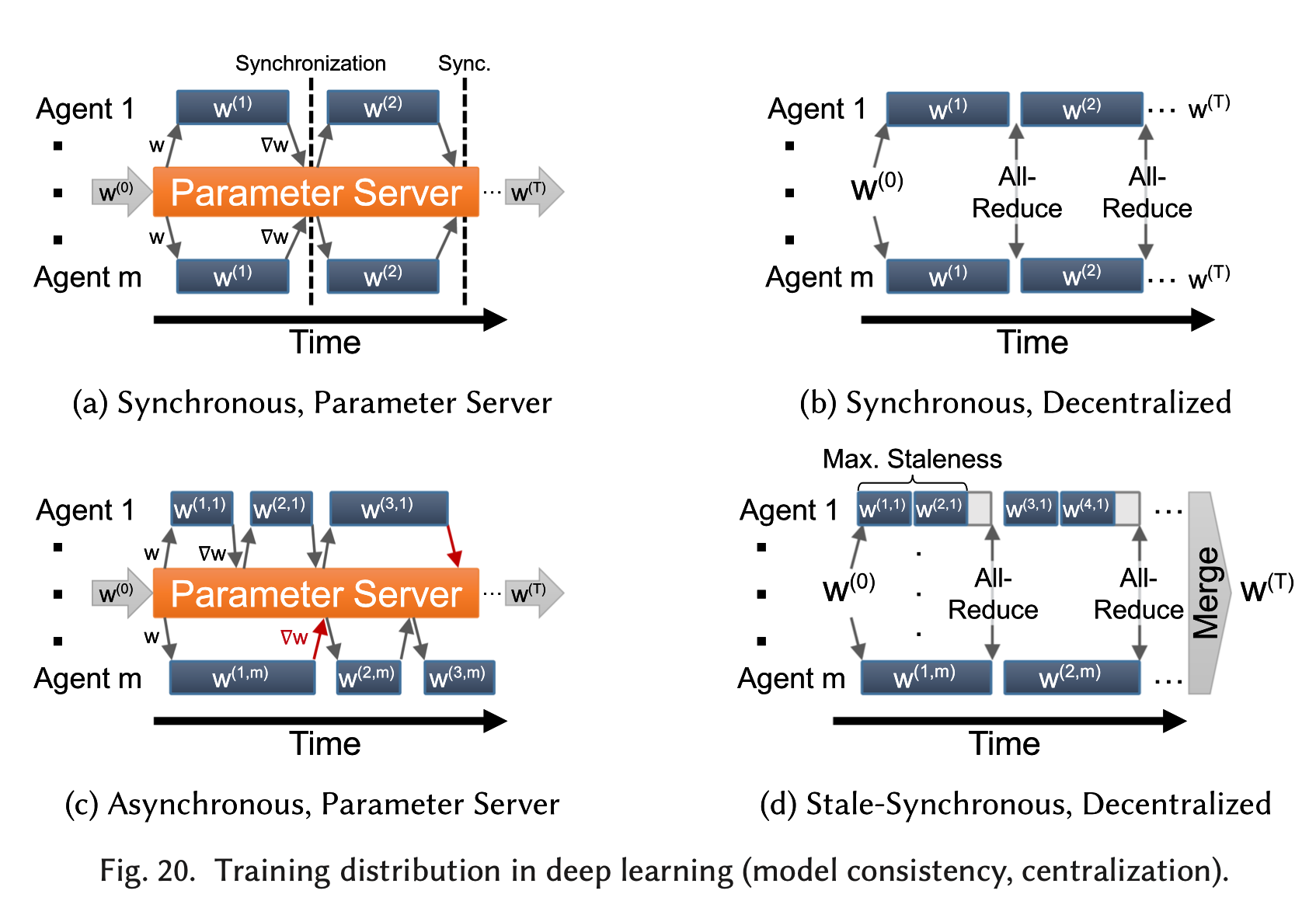
中心化的网络结构往往会包括一个参数服务器（Parameter Server）（20(a)(c)），参数服务器可能由一个或多个节点组成，由参数服务器担任所有计算节点的中介，统一收集所有计算节点的梯度值并计算参数更新，再发送给所有计算节点。去中心化的网络结构（20(b)(d)）则依赖于all-reduce操作在节点之间交换参数更新。

文章[20]指出，设计中心化还是去中心化的DNN训练的网络结构，取决于很多因素，包括：网络拓扑、带宽、延迟、参数更新频率、容错机制等等。

• 中心化

  最早提出参数服务器这个概念的文章是[21]，随后，最为著名的是李沐的文章[22]，他们提出了PS架构的第三代开源实现，针对机器学习应用的特点进行了再设计，使得针对机器学习的分布式应用的构建更为简洁。他们实现的PS架构高效、灵活并且robust。

  

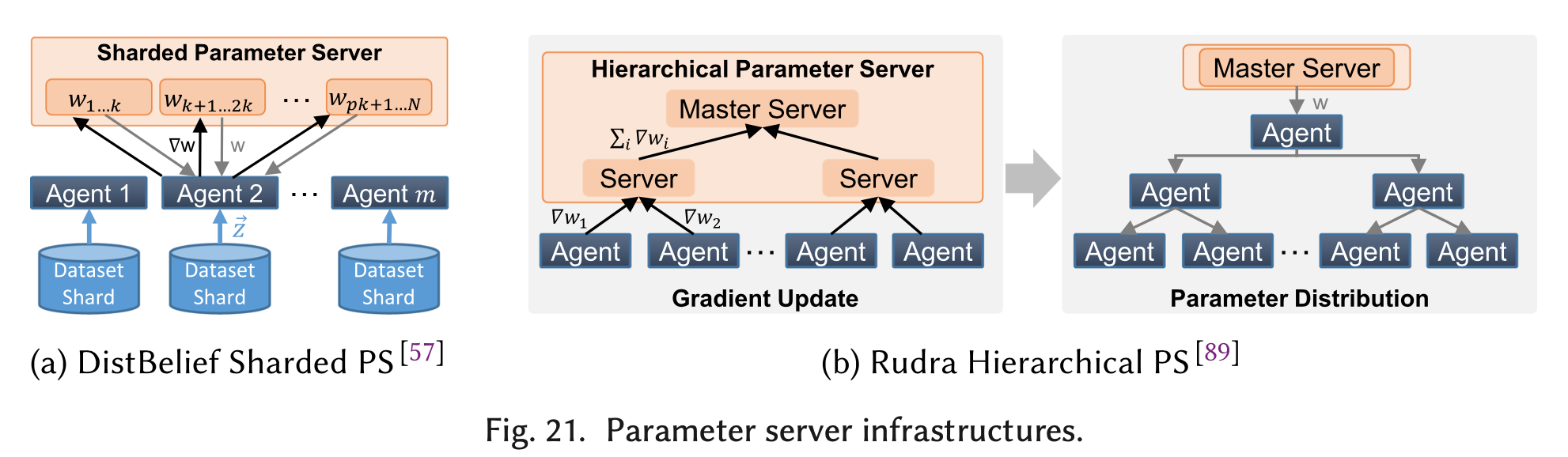
  参数服务器是一个抽象的概念，并不一定是一台服务器。分片化参数服务器Sharded PS[23] [24]（图21(a)）把权重参数分布到多个节点上存储，这样做减轻了参数服务器的拥挤程度，每个训练节点从相应的分片上获取并更新对应的权重参数。另一种层级化的PS架构[25] [26]（图21(b)）进一步缓解了资源的冲突。

  参数服务器架构不仅对性能有好处，也有益于容错机制的实现。机器学习中最简单的容错方案是checkpoint/restart，周期性地同步并把参数保存到非易失性存储，这很容易用PS架构来实现。DistBelief[23] [27]也对容错进行了更深入的研究，通过引入冗余计算、复制参数服务器提高了训练的弹性。参数服务器不仅可以减少本地存储开销，Project Adam[24]表明通过在参数服务器执行一些计算，可以使得节点之间的数据传输量更少。参数服务器也更容易处理异构的训练节点和网络设置。

• 去中心化

  在去中心化的架构中，通过使用异步训练，更容易实现负载平衡。在非一致性、去中心化的参数更新时，一种方案是使用一个固定的交流图[28]，实现基于邻居的参数/梯度交换。另一种方案是使用Gossip算法，每个节点会跟固定数量的随机节点进行数据交换。

模型一致性

另一种改善数据传输开销的方式是异步地进行参数更新。同步更新得到的是一致性模型，异步更新得到非一致性模型。同步更新的收敛性更好，但同步更新往往需要等待最慢的节点，可能引入大量的同步开销，而异步更新虽然会引入一些误差，但总的时间开销更短。文章[29]详细分析了stragglers对同步更新的影响，以及gradient staleness对异步更新的影响。

一致性模型（同步的）：每一个计算节点都能拿到最新的权重参数（图20(a)(b)）。即所有的节点在开始计算下一个minibatch之前都要互相交换他们得到的updates（交换的过程可以是中心化的，也可以是去中心化的）。

非一致性模型（异步的）：每一个计算节点所拥有的权重不一定是最新的(图20(c))。对于计算节点$i$，在时间t所拥有的权重参数记为$w^{(\tau, i)}$ ，$\tau \leq t$， $(t-\tau)$被称为staleness（or lag）。异步更新的SGD最早的文章是[30]。比较著名的非一致性SGD算法是HOGWILD共享内存算法[31]，文章证明了HOGWILD对稀疏的学习问题是收敛的，其他文章[32] [33]也证明了HOGWILD对凸优化和非凸优化问题是收敛的。HOGWILD最初是为shared-memory系统设计的，后来也被延伸到distributed-memory系统中使用[23] [34]。

为了在异步更新时保证正确性，Stale-Synchronous Parallelism (SSP)[35]在一致性模型和非一致性模型之间提出了一个折中方案(图20(d))。当一个计算节点达到了最大的staleness，强制性地执行一次全局同步，从而将staleness限定在一定的界限内。文章[29]提出了另一种折中方案，通过引入backup workers（直接丢弃最慢的一部分worker的结果），缓解了同步更新的同步开销，同时避免了引入异步更新的staleness。

其他

数据并行的一个重要的参数就是minibatch size。文章[36]对batch size对训练时间的影响给出了比较深入的分析。主要规律是，增加batch size最初会减少训练的步数，但收益会逐渐减小，直到增加batch size再也不会减少训练步数为止。

限制了batch size的一个瓶颈就是Batch Normalization op，因此有些工作针对数据并行的特点对BN op进行了重新的设计，从而增强数据并行的可扩展性。最近的工作把minibatch size增加到了8k [37]，32k [38]，甚至64k [39]。

有很多粗粒度的数据并行工作是基于MapReduce来设计的。例如ParallelSGD [40]、文章[41]、文章[42]、文章[43]。使用MapReduce很容易把并行的任务调度到不同的计算节点上，但很难进行DNN-specific的优化，因此很多工作使用MPI来设计细粒度的数据并行。例如，通过异步执行和流水线来减少延迟[44]、把mini-batch拆分为micro-batch[45] [46]。

模型并行

模型并行相对数据并行来说，更加复杂，也更难被实际应用。其核心思想是，将一个神经网络切分成多个部分，每个部分单独部署到某个计算设备上，每个计算设备只负责它被分配到的那一部分网络的训练，由多个计算设备共同完成对一个神经网络的训练过程。

模型并行相对于数据并行的优点是，能处理规模更大的网络。某些规模较大的神经网络不能被单个计算设备容纳，因此无法采用数据并行的方案，却可以采用模型并行。同时，模型并行使得神经网络的不同部分在不同的计算节点上被计算，这可以节省内存开销（每个计算节点不需要保存整个网络），但由于神经网络层与层之间存在数据依赖，因此模型并行会引入额外的数据传输开销。

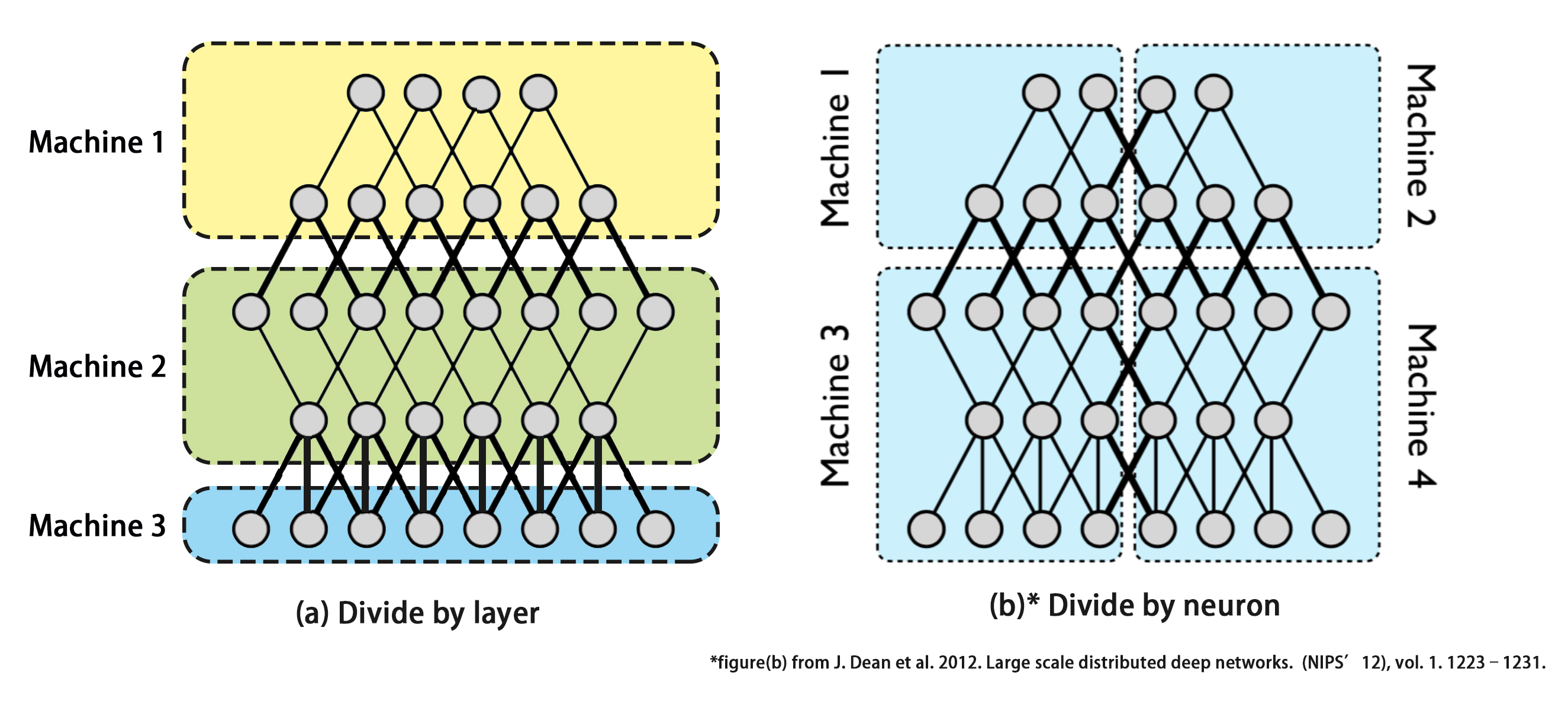
模型并行可以根据划分的粒度分为两大类，一类是按照layer粒度来划分（图(a)），另一类是按照neuron （神经元）粒度来划分（图(b)）。神经网络一般由很多_op_组成，每个_op_可以理解为由很多_neuron_组成的_layer_，一个_op_接收一个或多个_Tensor_进行计算后输出一个_Tensor_，这个过程其实是由该_layer_中的每个_neuron_对输出_Tensor_的相应的值进行计算，合并起来组成输出的Tensor。第一类模型并行的方案就是把每个_layer_作为一个整体部署到不同的设备上，也就是_op_划分，组成该layer的所有neuron就会被统一划分到相同设备上，这是比较粗粒度的划分方案。第二类方案就是把每一个_layer_划分为几部分，即把组成该layer的neuron分为几部分部署到不同的设备上，也就是neuron划分，每个设备上的不同部分针对输入该_layer_的_Tensor_的不同部分进行计算，是比较细粒度的划分方案。

op划分

按照op粒度寻找最优的分割方式的问题，也被称为“op放置问题”（device placement problem）。

因为神经网络是一种前后计算单元存在严重数据依赖的计算模型，因此当我们把神经网络按照op的粒度切割成几部分部署到不同的计算设备上时，每一个计算设备都要等待上一个计算设备完成计算后，将神经网络的中间结果传输过来，才能开始计算。这个过程其实不是并行执行的，而是串行的，实现了“分布式计算”而并没有实现“并行计算”。因此，可以认为，op划分解决了“单个设备装不下整个网络”的问题，却没有对神经网络的训练过程起到加速的作用。不过，在某些存在并行结构的网络上，op划分理论上确实可以实现“并行加速”。例如在Inception网络中，存在大量的多分支网络块，每个分支之间不存在数据依赖，对于这样的结构，如果将多个分支部署到不同的计算设备上，理论上可以实现训练过程的加速，但在实际部署进行训练时，需要考虑数据传输开销，不一定能实现训练的加速。

关于op划分 的研究并不是很多，可能的原因是单个设备“装不下”的神经网络并不多，存在“并行结构”的网络也不多，导致该并行方案的适用场景较少。

在已有的研究中，最著名的是Google提出的基于强化学习的op放置问题优化方案[47]，他们使用一个强化学习模型来寻找最优的划分方案，在这之后他们进一步优化了自己的工作，在对神经网络进行划分之前，先用另一个强化学习模型对op进行分组，分组后，大大减少了强化学习模型需要处理的op数量，从而得到了一个分层的强化学习模型[48]。他们的工作在RNNLM、NMT和Inception-V3三种网络上得到了比人工专家更好的划分方案，但观察他们的结果可以发现，在某些情况下，多个GPU并不能带来性能提升，强化学习模型最终给出的方案仍是把所有op全部放在同一个设备上。

基于Google的工作，有另一个研究团队进一步做了更多的工作。他们首先提出了Spotlight[49]，优化了Google的强化学习算法，使用_Proximal Policy_，而不是_Gradient Policy_。同时，他们还对“op放置问题”做了理论上的进一步抽象，提炼为一个马尔科夫决策过程。他们进一步提出了Post[50]，结合了_Proximal Policy_和_Cross-entropy Minimization_（一种采样策略），最终他们的方法得到的部署方案能实现比Google的部署方案短63.7%的训练时间。

不过以上工作有个问题就是，没有神经网络的性能预测模型。强化学习模型每次训练需要用到目标神经网络的运行时间作为奖励值，他们通过真实部署并运行实际的模型来得到运行时间，这部分时间开销是十分巨大的。

neuron划分

从neuron的角度进行划分，也可看做是对Tensor进行划分。把神经网络每一层的不同神经元划分到不同的计算节点，也就是把一个4d的tensor在Channel、Height、Width维度上进行划分（数据并行是划分Sample维度）。

相比op划分的优点是，可以使得多个设备之间的负载更加均衡。代表性的文章是Eurosys’19的Tofu[51]，抽象出了Tensor划分的模式：partition-n-reduce。_partition-n-reduce_的意思是，神经网络中的op $c$ 可以被并行到多个设备上执行，每个设备上执行的是一样的$c$，但仅对输入数据的一部分进行计算，最终的输出tensor $O$ 可以由两种方式得到：1)$O$是每个设备上的op $c$ 输出tensor在某个维度上的拼接；2)$O$是每个设备上的op $c$输出的tensor的element-wise的reduction。

斯坦福团队的文章[52]对于单个神经网络层从_height/width/channel_等维度进行划分。Sysml’19的文章Beyond[53]是斯坦福团队进一步的工作，他们提出了一种 _“超越数据并行和模型并行”_的方案，其核心思想是，提出了一个更大的搜索/模型划分空间，以前的数据并行是从_Sample_的维度进行划分，模型并行是从_Parameter_的维度进行划分，现在他们的框架不仅能从_Sample_和_Parameter_的维度进行划分，还能从_Operator_和_Attribute_的维度进行划分，于是构成了一个被称作_SOAP_的搜索空间。在我看来，其实SOAP搜索空间里的Operator和Parameter仍是模型并行的范畴，Attribute确实跟模型并行不太一样，以卷积op为例，Attribute指的是输入数据内部的某些维度，比如图片的width和height，在这两个维度上对数据进行划分后，不同的设备是在输入图片的一部分区域进行卷积，这时，每个设备上仍然有当前op的全部参数（根据卷积的定义，即使只计算一部分区域，仍然需要全部的卷积核参数），因此，模型并未被拆分，拆分的是数据。而如果从输入图片的channel维度进行划分，情况就有所不同，因为对于不同channel的卷积需要的是不同的卷积核，这时，不同的设备被分配到了所有卷积核参数的一部分，此时属于模型并行。

除此之外，他们还提出了一个用来对神经网络运行时间进行模拟的simulator。这个simulator不对单个op的运行时间进行预测，而是直接profiling得到每个op的运行时间。对于整个神经网络，这个simulator将其抽象为一个_任务图_，从而能够比较清晰地知道不同任务（此处的任务已经是被划分后的op）的起止时间，是否冲突，从而能用一些搜索算法找到任务分布式部署的最优解。他们的simulator的预测时间误差在30%以内。

斯坦福的工作与Tofu其实有很多相同点。虽然两篇文章的表述不同，但其实都是neuron粒度的划分方案。FlexFlow的Parameter和Attribute维度在Tofu的文中都有体现。

几篇文章的不同点是，Tofu是基于现有的深度学习框架MXNet设计的，而FlexFlow是自己设计实现了新的框架（基于Legion）。同时，Tofu提出了一种新的描述性语言TDL(Tensor Description Language)，通过框架对每个tensor的分析得出划分的并行度，而FlexFlow要求用户人为地指定并行度。总的来说，Tofu比FlexFlow更加地通用。

对神经网络进行neuron粒度的划分，会在划分边界产生halo exchange的问题，即边界神经元需要用到邻近神经元的信息，从而产生了数据交换。文章[19]也从height、width维度实现了neuron划分，并且通过overlap halo exchange以及计算过程，实现了加速。另外，文章[54]提出了Tiled and Locally-Connected Networks，通过把卷积核分解来缓解halo exchanges的问题。LCN不存在权重共享，但权重共享是CNN一大特点，因此LCN并不常用。

混合并行（结合数据并行和模型并行）

在很多时候，数据并行和模型并行并不是对立的，而是要结合起来使用的。对多种并行方式的混合使用，可以克服其中每种方式的不足。

文章[55]提出的一种思路是，按照神经网络的不同层来采用不同的并行方案，例如，存在密集连接的具有大量参数的层，如全连接层，更倾向于使用模型并行来减少参数同步的开销；而卷积层和池化层更倾向于使用数据并行来排除来自前一层的数据传输。文章[56]也适用了类似的方案，并从理论上分析了communication cost。

另一个例子是AMPNet[44]。AMPNet是CPU上的DNN训练的异步实现。AMPNet使用了中间表示来实现细粒度的模型并行。层内和层间的并行任务被异步调度。并且，动态控制流的异步执行使得前向计算、后向更新、权重更新可以被流水化。

几个采用了混合并行来构建的大规模深度学习框架是：

DistBelief[23]。DistBelief分布式系统结合了三类并行策略。训练过程是在模型的多个复制上同时进行的，每个复制采用不同的数据进行训练（数据并行）。在每个复制中，模型同一层的不同神经元是分布式部署的（模型并行），不同层之间也是并行的（流水线并行）。

Project Adam[24]也采用了类似的思想。先是对整个网络垂直切分，即按照neuron粒度把每个layer划分到不同的设备上，因为这会最小化机器间的数据传输。在每个机器内部通过多线程实现了数据并行，每个线程计算不同的图片，异步且无锁地更新权重。

流水线并行

在前文_op划分_部分，我们讲到，如果对神经网络进行op划分，其实这并没有使得整个神经网络被“并行计算”，因为前后的op存在数据依赖。这个现象很像计算机中指令的执行过程，在5级流水CPU中，一条指令被分为5个阶段来执行，前后阶段存在数据依赖，在不引入流水线时，很多的部件会有大量的闲置和等待时间，一旦引入流水线，不仅部件的利用率增大了，而且总的执行时间也减少了。

数据并行、模型并行都可以看做是对一个batch内的数据并行计算（intra-batch parallelization）。而流水线并行可以看做是在batch之间实现了并行（inter-batch parallelization）。

Google提出了GPipe[57]，将每次训练的mini-batch拆分为多个micro-batch，流水线的每个阶段计算一个micro-batch。在多个micro-batch完成后进行同步，相当于每个mini-batch同步一次，是同步更新。不存在异步更新造成的参数污染问题。

PipeDream[58]则提出了流水线的另一种实现。PipeDream使用异步更新，能保持硬件资源最大化利用，流水线效率更高。但为了保证神经网络计算的正确性，同一个mini-batch的前向计算和后向计算过程必须使用同一个版本参数。因此，PipeDream会在每个节点存储多个版本的参数。同时，由于流水线各个阶段的运行时间越接近，整个流水线的并行效率就越高，PipeDream提出了一套自动划分机制，通过一个快速的profiling过程来决定如何划分op。由于某些op跟其他op的运行时间相差实在太大，PipeDream也会在某些op使用数据并行，来使得整个网络各个layer的时间更加均衡。

最优部署策略的搜索问题

为了寻找最优的分布式划分/部署方案，往往存在一个巨大的搜索空间，如何高效地找到最优的解，不同的文章采用了不同的方法。例如，[47]采用了强化学习。[19] **使用了图的最短路径算法、[52]使用了贪心算法、[53]使用了马尔科夫-蒙特卡洛搜索算法、[51]**使用了动态规划算法。

• 动态规划

  文章[13]存在的搜索问题是，在分布式的环境中，如何找到最优的系统配置参数，使得单个epoch的训练时间最短，他们的问题空间既包含数据并行，也包含模型并行。

  简单地说，他们设计的策略就是用贪心算法寻找work-resource 的mapping（把神经网络的哪部分放到哪个设备上），用动态规划算法寻找对网络的切分。既然是动态规划，就有DP-equation：

  

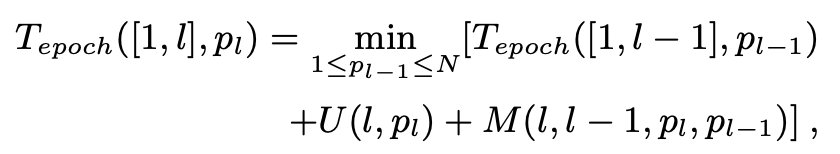
  $T_{epoch} ([1,l],p_l)$ 是从layer 1 到 layer $l$ 的总时间，layer $l$ 有 $p_l$ 个partition。$U(l, p_l)$ 是layer $l$ 的计算时间。$M(l, l-1, p_l, p_{l-1})$ 是layer $l-1$ 和 layer $l$ 之间的数据传输时间。

• 强化学习

  文章[47]面临的问题是，对于分布式环境中的一个神经网络，把每个op放到哪个设备上能带来最好的性能。这篇文章采用了强化学习。强化学习只是一个学习策略，而他们要训练的模型是一个LSTM循环神经网络。他们这个循环神经网络每次读入一个序列的op信息，输出每个op放在哪个设备的结果。然后真实地按照LSTM输出的结果部署整个网络并运行，测得运行时间，用这个运行时间作为强化学习的reward，来对LSTM进行训练。

  文章[49]进一步优化了强化学习的算法，使用了_Proximal Policy_，而不是_Gradient Policy_，得到了更好的效果。

• 马尔科夫-蒙特卡洛

  文章[53]面临的搜索问题是，对于给定的operator graph和device toppology，找到SOAP搜索空间中最高效的并行策略。可以通过归约到minimum makespan问题，证明这是NP-hard的问题。这篇文章使用了Metropolis-Hastings算法，简单地说就是每一步基于目前的并行策略进行一定的随机化修改，得到新的策略，利用Performance Model对新的并行策略进行时间的预测，根据新旧策略的时间预测值，按照一定的概率接受新的并行策略。终止条件是，搜索时间budget耗尽，或者有一半的搜索时间都没有得到新的改进。

• 贪心算法

  文章[52]面临的搜索问题是，对于一个神经网络想要构造layer-wise的并行策略，即在每个layer采用不同的并行策略，最终使得整个网络时间最短。他们采用的做法是，设计了一个图归约算法，通过节点删除、边删除两个策略将完整的神经网络归约为简化的神经网络，再对简化网络中每一层可能的并行策略进行枚举，找到最优的策略后，再进行图归约的逆操作，寻找每个节点的最优并行策略。他们通过证明，表示这样的过程找到的layer-wise策略是最优的。这个算法本质上就是贪心算法。

• 图最短路径算法

  文章[19]面临的搜索问题是，想要寻找一个layer-wise的并行策略（与上一小节类似），他们采取的方法是，首先对于每个layer按照一定的Heuristic给出可能的并行策略，然后构造一个图，从layer $i$ 的每种策略生成一条边到child layer $j$ 的每一种策略，边的权重就是layer $i$ 该并行策略按照Performance model 给出的时间预测值。然后对这个构造出的图，寻找从第一个layer到最后一个layer的最短路径。由于是有向无环图，所以可以在线性时间内被找到。同时，如果对于某些layer有大量的候选策略，可以设计一定的剪枝策略进行优化。这样的算法似乎本质上也是贪心算法。

针对数据传输的优化

前面已经提到，在分布式深度学习训练的过程中，数据传输的开销往往是限制了不能大规模扩展的瓶颈。有很多工作已经被提出，用于对数据传输进行优化。主要分为两大类：（1）减少消息的大小和数量；（2）优化消息的传输顺序，Overlap消息传输过程和计算过程。

第一类，又可分为两个分支：量化和稀疏化。第二类，主要是设计communication scheduler。

量化 Quantization

量化就是把连续的信息映射到表示一组（或一个范围的）值的buckets中。文章[59]指出，参数和梯度的值的分布范围往往较窄，因此量化方法可以比较有效地减少每个参数的表示位数。

量化可以用于训练过程[60] [61] [62]，也可以用于推理过程[63] [64]，把训练后的参数量化表示。

量化通常是通过减少浮点数的位数来实现的[32] [60] [61]，例如把32位浮点数转化为16位浮点数（半精度）。减少位数的方式并不能直接被应用，往往还需要对参数进行四舍五入，[61]提出了随机四舍五入方法，使得参数值满足正确的期望值。[65]使用了Huffman编码在不降低收敛性的前提下提高存储效率。此外，还有一些工作将将网络量化为二进制参数、三进制参数、三进制梯度、二进制参数+三进制梯度等等形式。

稀疏化 Sparsification

DNN（尤其是CNN）在参数更新时的梯度是比较稀疏的，并不是每个参数都需要更新。

第一个利用稀疏化梯度的应用是[66]，设置一个固定的threshold，低于threshold的值不会被送出。之后的一些工作提出了相对的以及适应性的threshold，目的都是只传输“重要”的值。

在中心化的网络架构中，稀疏化很容易实现，稀疏化的消息直接在PS和agents之间交换，而去中心化的网络架构中，每个节点可能得到梯度不同维度的更新，Kylix[67]用两个步骤实现了稀疏化的allreduce：第一步交换indices，第二步交换数据。SparCML[68]则支持索引值任意改变的allreduce操作。

调度优化 Communication Scheduler

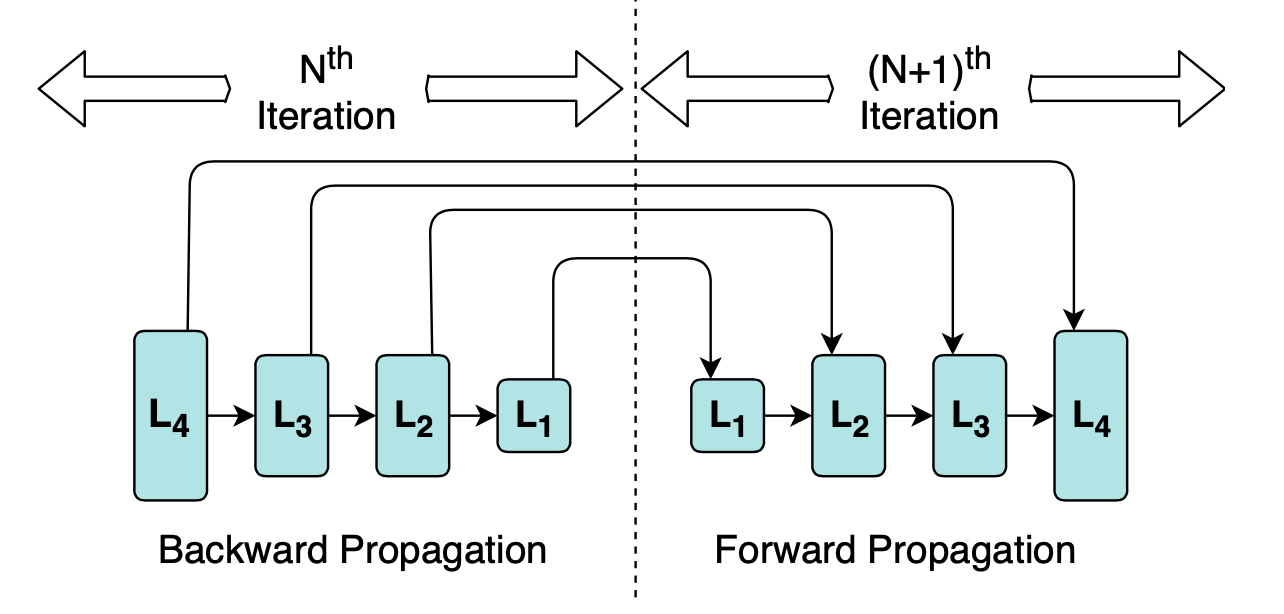
P3（Priority-based Parameter Propagation）[69]提出，在一般的神经网络训练过程中，是按层进行参数的更新，而且在后向计算过程中最先被计算完成的layer的参数，在下一个迭代过程中，最后被使用。因此，把参数被使用的先后顺序纳入考虑范围，并且对参数进行分片，可以使带宽更高效地被利用，因此该篇文章为参数引入了更新优先级，并在MXNet上进行了实现，得到了更好的性能。

TicTac[70]是一个类似的工作，也是对参数进行有优先级的更新。不过这篇文章给出了两种heuristics，TIC和TAC。TIC是Timing-Independent Communication scheduling，TAC是Timing-Aware Communication scheduling。区别在于赋予优先级时，是否考虑op运行时间的因素。

字节跳动团队的ByteScheduler[71]，是结合了以上两篇文章的特点，结合了priority-based communication scheduling以及tensor partitioning，推出的通用性communication scheduler。其通用性体现在，不仅支持多种机器学习框架，也支持多种数据并行架构，例如PS、all-reduce。他们之所以能实现通用性，是因为他们引入了一个统一的中间表示层Dependency Proxy，有了这个中间表示，他们就不需要去修改各个机器学习框架的源码，而是直接以插件的形式把scheduler引入相应的框架之中。

其他方法

Project Adam通过发送activations和errors而不是参数本身，来减小全连接层的内存占用。Petuum框架[72] [73] [74]进一步延伸这个方法，传输分解后的外积，将这个思想一般化为Sufficient Factor Broadcasting (SFB) [75]

另一种减少DNN内存占用的方法是，设计特殊的DNN结构。例如，构造1x1卷积层[76]，对卷积的tensor进行reshaping[77]或采用Tucker Decomposition[78]、可分解的卷积[79] [80]。

参考文献

[1] Robbins, H., & Monro, S. (1951). A stochastic approximation method. The annals of mathematical statistics, 400-407.
[2] Oyama, Y., Nomura, A., Sato, I., Nishimura, H., Tamatsu, Y., & Matsuoka, S. (2016, December). Predicting statistics of asynchronous SGD parameters for a large-scale distributed deep learning system on GPU supercomputers. In 2016 IEEE International Conference on Big Data (Big Data) (pp. 66-75). IEEE.
[3] Demmel, J., & Dinh, G. (2018). Communication-optimal convolutional neural nets. arXiv preprint arXiv:1802.06905.
[4] Cong, J., & Xiao, B. (2014, September). Minimizing computation in convolutional neural networks. In International conference on artificial neural networks (pp. 281-290). Springer, Cham.
[5] Vasilache, N., Johnson, J., Mathieu, M., Chintala, S., Piantino, S., & LeCun, Y. (2014). Fast convolutional nets with fbfft: A GPU performance evaluation. arXiv preprint arXiv:1412.7580.
[6] Lavin, A., & Gray, S. (2016). Fast algorithms for convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 4013-4021).
[7] Chetlur, S., Woolley, C., Vandermersch, P., Cohen, J., Tran, J., Catanzaro, B., & Shelhamer, E. (2014). cudnn: Efficient primitives for deep learning. arXiv preprint arXiv:1410.0759.
[8] Li, C., Yang, Y., Feng, M., Chakradhar, S., & Zhou, H. (2016, November). Optimizing memory efficiency for deep convolutional neural networks on GPUs. In SC’16: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis(pp. 633-644). IEEE.
[9] Appleyard, J., Kocisky, T., & Blunsom, P. (2016). Optimizing performance of recurrent neural networks on gpus. arXiv preprint arXiv:1604.01946.
[10] Gruslys, A., Munos, R., Danihelka, I., Lanctot, M., & Graves, A. (2016). Memory-efficient backpropagation through time. In Advances in Neural Information Processing Systems (pp. 4125-4133).
[11] Chen, T., Xu, B., Zhang, C., & Guestrin, C. (2016). Training deep nets with sublinear memory cost. arXiv preprint arXiv:1604.06174.
[12] Diamos, G., Sengupta, S., Catanzaro, B., Chrzanowski, M., Coates, A., Elsen, E., … & Satheesh, S. (2016, June). Persistent rnns: Stashing recurrent weights on-chip. In International Conference on Machine Learning (pp. 2024-2033).
[13] Yan, F., Ruwase, O., He, Y., & Chilimbi, T. (2015, August). Performance modeling and scalability optimization of distributed deep learning systems. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 1355-1364).
[14] Qi, H., Sparks, E. R., & Talwalkar, A. (2016). Paleo: A performance model for deep neural networks.
[15] Cai, E., Juan, D. C., Stamoulis, D., & Marculescu, D. (2017). Neuralpower: Predict and deploy energy-efficient convolutional neural networks. arXiv preprint arXiv:1710.05420.
[16] Justus, D., Brennan, J., Bonner, S., & McGough, A. S. (2018, December). Predicting the computational cost of deep learning models. In 2018 IEEE International Conference on Big Data (Big Data) (pp. 3873-3882). IEEE.
[17] Song, M., Hu, Y., Chen, H., & Li, T. (2017, February). Towards pervasive and user satisfactory CNN across GPU microarchitectures. In 2017 IEEE International Symposium on High Performance Computer Architecture (HPCA) (pp. 1-12). IEEE.
[18] Simonyan, K., & Zisserman, A. (2014). Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556.
[19] Dryden, N., Maruyama, N., Benson, T., Moon, T., Snir, M., & Van Essen, B. (2019, May). Improving strong-scaling of CNN training by exploiting finer-grained parallelism. In 2019 IEEE International Parallel and Distributed Processing Symposium (IPDPS) (pp. 210-220). IEEE.
[20] Lian, X., Zhang, C., Zhang, H., Hsieh, C. J., Zhang, W., & Liu, J. (2017). Can decentralized algorithms outperform centralized algorithms? a case study for decentralized parallel stochastic gradient descent. In Advances in Neural Information Processing Systems (pp. 5330-5340).
[21] Smola, A., & Narayanamurthy, S. (2010). An architecture for parallel topic models. Proceedings of the VLDB Endowment, 3(1-2), 703-710.
[22] Li, M., Andersen, D. G., Park, J. W., Smola, A. J., Ahmed, A., Josifovski, V., … & Su, B. Y. (2014). Scaling distributed machine learning with the parameter server. In 11th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 14) (pp. 583-598).
[23] Dean, J., Corrado, G., Monga, R., Chen, K., Devin, M., Mao, M., … & Le, Q. V. (2012). Large scale distributed deep networks. In Advances in neural information processing systems (pp. 1223-1231).
[24] Chilimbi, T., Suzue, Y., Apacible, J., & Kalyanaraman, K. (2014). Project adam: Building an efficient and scalable deep learning training system. In 11th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 14)(pp. 571-582).
[25] Gupta, S., Zhang, W., & Wang, F. (2016, December). Model accuracy and runtime tradeoff in distributed deep learning: A systematic study. In 2016 IEEE 16th International Conference on Data Mining (ICDM) (pp. 171-180). IEEE.
[26] Yu, Y., Jiang, J., & Chi, X. (2016, December). Using supercomputer to speed up neural network training. In 2016 IEEE 22nd International Conference on Parallel and Distributed Systems (ICPADS) (pp. 942-947). IEEE.
[27] Le, Q. V. (2013, May). Building high-level features using large scale unsupervised learning. In 2013 IEEE international conference on acoustics, speech and signal processing (pp. 8595-8598). IEEE.
[28] Lian, X., Zhang, W., Zhang, C., & Liu, J. (2017). Asynchronous decentralized parallel stochastic gradient descent. arXiv preprint arXiv:1710.06952.
[29] Chen, J., Pan, X., Monga, R., Bengio, S., & Jozefowicz, R. (2016). Revisiting distributed synchronous SGD. arXiv preprint arXiv:1604.00981.
[30] Tsitsiklis, J., Bertsekas, D., & Athans, M. (1986). Distributed asynchronous deterministic and stochastic gradient optimization algorithms. IEEE transactions on automatic control, 31(9), 803-812.
[31] Recht, B., Re, C., Wright, S., & Niu, F. (2011). Hogwild: A lock-free approach to parallelizing stochastic gradient descent. In Advances in neural information processing systems (pp. 693-701).
[32] De Sa, C. M., Zhang, C., Olukotun, K., & Ré, C. (2015). Taming the wild: A unified analysis of hogwild-style algorithms. In Advances in neural information processing systems (pp. 2674-2682).
[33] Lian, X., Huang, Y., Li, Y., & Liu, J. (2015). Asynchronous parallel stochastic gradient for nonconvex optimization. In Advances in Neural Information Processing Systems (pp. 2737-2745).
[34] Noel, C., & Osindero, S. (2014, December). Dogwild!-distributed hogwild for cpu & gpu. In NIPS Workshop on Distributed Machine Learning and Matrix Computations (pp. 693-701).
[35] Ho, Q., Cipar, J., Cui, H., Lee, S., Kim, J. K., Gibbons, P. B., … & Xing, E. P. (2013). More effective distributed ml via a stale synchronous parallel parameter server. In Advances in neural information processing systems (pp. 1223-1231).
[36] Shallue, C. J., Lee, J., Antognini, J., Sohl-Dickstein, J., Frostig, R., & Dahl, G. E. (2018). Measuring the effects of data parallelism on neural network training. arXiv preprint arXiv:1811.03600.
[37] Goyal, P., Dollár, P., Girshick, R., Noordhuis, P., Wesolowski, L., Kyrola, A., … & He, K. (2017). Accurate, large minibatch sgd: Training imagenet in 1 hour. arXiv preprint arXiv:1706.02677.
[38] You, Y., Gitman, I., & Ginsburg, B. (2017). Large batch training of convolutional networks. arXiv preprint arXiv:1708.03888.
[39] Smith, S. L., Kindermans, P. J., Ying, C., & Le, Q. V. (2017). Don’t decay the learning rate, increase the batch size. arXiv preprint arXiv:1711.00489.
[40] Zinkevich, M., Weimer, M., Li, L., & Smola, A. J. (2010). Parallelized stochastic gradient descent. In Advances in neural information processing systems (pp. 2595-2603).
[41] Jiang, J., Cui, B., Zhang, C., & Yu, L. (2017, May). Heterogeneity-aware distributed parameter servers. In Proceedings of the 2017 ACM International Conference on Management of Data (pp. 463-478).
[42] Le, Q. V., Ngiam, J., Coates, A., Lahiri, A., Prochnow, B., & Ng, A. Y. (2011). On optimization methods for deep learning.
[43] Zhang, K., & Chen, X. W. (2014). Large-scale deep belief nets with mapreduce. IEEE Access, 2, 395-403.
[44] Gaunt, A. L., Johnson, M. A., Riechert, M., Tarlow, D., Tomioka, R., Vytiniotis, D., & Webster, S. (2017). AMPNet: Asynchronous model-parallel training for dynamic neural networks. arXiv preprint arXiv:1705.09786.
[45] Oyama, Y., Ben-Nun, T., Hoefler, T., & Matsuoka, S. (2018, September). Accelerating deep learning frameworks with micro-batches. In 2018 IEEE International Conference on Cluster Computing (CLUSTER) (pp. 402-412). IEEE.
[46] Zlateski, A., Lee, K., & Seung, H. S. (2016, November). ZNNi: maximizing the inference throughput of 3D convolutional networks on CPUs and GPUs. In SC’16: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (pp. 854-865). IEEE.
[47] Mirhoseini, A., Pham, H., Le, Q. V., Steiner, B., Larsen, R., Zhou, Y., … & Dean, J. (2017, August). Device placement optimization with reinforcement learning. In Proceedings of the 34th International Conference on Machine Learning-Volume 70 (pp. 2430-2439). JMLR. org.
[48] Mirhoseini, A., Goldie, A., Pham, H., Steiner, B., Le, Q. V., & Dean, J. (2018). A hierarchical model for device placement.
[49] Gao, Y., Chen, L., & Li, B. (2018, July). Spotlight: Optimizing device placement for training deep neural networks. In International Conference on Machine Learning (pp. 1676-1684).
[50] Gao, Y., Chen, L., & Li, B. (2018). Post: Device placement with cross-entropy minimization and proximal policy optimization. In Advances in Neural Information Processing Systems (pp. 9971-9980).
[51] Wang, M., Huang, C. C., & Li, J. (2019, March). Supporting very large models using automatic dataflow graph partitioning. In Proceedings of the Fourteenth EuroSys Conference 2019(pp. 1-17).
[52] Jia, Z., Lin, S., Qi, C. R., & Aiken, A. (2018). Exploring hidden dimensions in parallelizing convolutional neural networks. arXiv preprint arXiv:1802.04924.
[53] Jia, Z., Zaharia, M., & Aiken, A. (2018). Beyond data and model parallelism for deep neural networks. arXiv preprint arXiv:1807.05358.
[54] Ngiam, J., Chen, Z., Chia, D., Koh, P. W., Le, Q. V., & Ng, A. Y. (2010). Tiled convolutional neural networks. In Advances in neural information processing systems (pp. 1279-1287).
[55] Krizhevsky, A. (2014). One weird trick for parallelizing convolutional neural networks. arXiv preprint arXiv:1404.5997.
[56] Ben-Nun, T., Levy, E., Barak, A., & Rubin, E. (2015, November). Memory access patterns: the missing piece of the multi-GPU puzzle. In SC’15: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (pp. 1-12). IEEE.
[57] Huang, Y., Cheng, Y., Bapna, A., Firat, O., Chen, D., Chen, M., … & Wu, Y. (2019). Gpipe: Efficient training of giant neural networks using pipeline parallelism. In Advances in Neural Information Processing Systems (pp. 103-112).
[58] Narayanan, D., Harlap, A., Phanishayee, A., Seshadri, V., Devanur, N. R., Ganger, G. R., … & Zaharia, M. (2019, October). PipeDream: generalized pipeline parallelism for DNN training. In Proceedings of the 27th ACM Symposium on Operating Systems Principles (pp. 1-15).
[59] Köster, U., Webb, T., Wang, X., Nassar, M., Bansal, A. K., Constable, W., … & Khosrowshahi, A. (2017). Flexpoint: An adaptive numerical format for efficient training of deep neural networks. In Advances in neural information processing systems (pp. 1742-1752).
[60] Dettmers, T. (2015). 8-bit approximations for parallelism in deep learning. arXiv preprint arXiv:1511.04561.
[61] Gupta, S., Agrawal, A., Gopalakrishnan, K., & Narayanan, P. (2015, June). Deep learning with limited numerical precision. In International Conference on Machine Learning (pp. 1737-1746).
[62] Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., & Bengio, Y. (2017). Quantized neural networks: Training neural networks with low precision weights and activations. The Journal of Machine Learning Research, 18(1), 6869-6898.
[63] Rastegari, M., Ordonez, V., Redmon, J., & Farhadi, A. (2016, October). Xnor-net: Imagenet classification using binary convolutional neural networks. In European conference on computer vision (pp. 525-542). Springer, Cham.
[64] Zhou, S., Wu, Y., Ni, Z., Zhou, X., Wen, H., & Zou, Y. (2016). Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients. arXiv preprint arXiv:1606.06160.
[65] Han, S., Mao, H., & Dally, W. J. (2015). Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv preprint arXiv:1510.00149.
[66] Strom, N. (2015). Scalable distributed DNN training using commodity GPU cloud computing. In Sixteenth Annual Conference of the International Speech Communication Association.
[67] Zhao, H., & Canny, J. (2014, September). Kylix: A sparse allreduce for commodity clusters. In 2014 43rd International Conference on Parallel Processing (pp. 273-282). IEEE.
[68] Renggli, C., Ashkboos, S., Aghagolzadeh, M., Alistarh, D., & Hoefler, T. (2019, November). Sparcml: High-performance sparse communication for machine learning. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (pp. 1-15).
[69] Jayarajan, A., Wei, J., Gibson, G., Fedorova, A., & Pekhimenko, G. (2019). Priority-based parameter propagation for distributed DNN training. arXiv preprint arXiv:1905.03960.
[70] Hashemi, S. H., Jyothi, S. A., & Campbell, R. H. (2018). TicTac: Accelerating distributed deep learning with communication scheduling. arXiv preprint arXiv:1803.03288.
[71] Peng, Y., Zhu, Y., Chen, Y., Bao, Y., Yi, B., Lan, C., … & Guo, C. (2019, October). A generic communication scheduler for distributed DNN training acceleration. In Proceedings of the 27th ACM Symposium on Operating Systems Principles (pp. 16-29).
[72] Xing, E. P., Ho, Q., Dai, W., Kim, J. K., Wei, J., Lee, S., … & Yu, Y. (2015). Petuum: A new platform for distributed machine learning on big data. IEEE Transactions on Big Data, 1(2), 49-67.
[73] Zhang, H., Hu, Z., Wei, J., Xie, P., Kim, G., Ho, Q., & Xing, E. (2015). Poseidon: A system architecture for efficient gpu-based deep learning on multiple machines. arXiv preprint arXiv:1512.06216.
[74] Zhang, H., Zheng, Z., Xu, S., Dai, W., Ho, Q., Liang, X., … & Xing, E. P. (2017). Poseidon: An efficient communication architecture for distributed deep learning on {GPU} clusters. In 2017 {USENIX} Annual Technical Conference ({USENIX}{ATC} 17) (pp. 181-193).
[75] Xie, P., Kim, J. K., Zhou, Y., Ho, Q., Kumar, A., Yu, Y., & Xing, E. P. (2016, June). Lighter-Communication Distributed Machine Learning via Sufficient Factor Broadcasting. In UAI.
[76] Iandola, F. N., Han, S., Moskewicz, M. W., Ashraf, K., Dally, W. J., & Keutzer, K. (2016). SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 0.5 MB model size. arXiv preprint arXiv:1602.07360.
[77] Li, D., Wang, X., & Kong, D. (2018, April). Deeprebirth: Accelerating deep neural network execution on mobile devices. In Thirty-second AAAI conference on artificial intelligence.
[78] Kim, Y. D., Park, E., Yoo, S., Choi, T., Yang, L., & Shin, D. (2015). Compression of deep convolutional neural networks for fast and low power mobile applications. arXiv preprint arXiv:1511.06530.
[79] Chollet, F. (2017). Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 1251-1258).
[80] Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D., Wang, W., Weyand, T., … & Adam, H. (2017). Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv preprint arXiv:1704.04861.
[81] Ben-Nun, T., & Hoefler, T. (2019). Demystifying parallel and distributed deep learning: An in-depth concurrency analysis. ACM Computing Surveys (CSUR), 52(4), 1-43.